Click here to read part 1, ‘Waves on a string’
Waves on a string
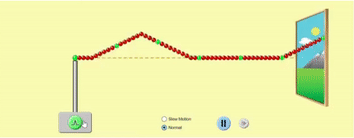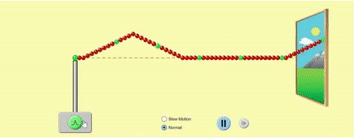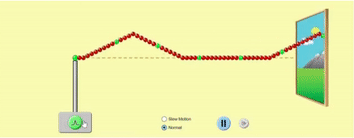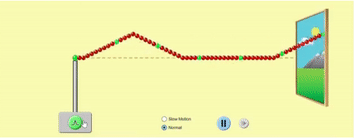
In the previous article, we looked at how a wave propagates along a stretched string. We can visualise it this way:
You are holding the left end of the string, and the other end is far, far away from you (so we can ignore wave reflection for now). In the GIF above, the string is shown as going into the distance through a window. When you cause a small disturbance in the string at the left end, the disturbance travels through the string along its length towards right.
Damping
Ideally, no energy is lost in this process, and all the energy from the initial displacement is transferred through the wave along the length of the string. However, in practice, some energy is dissipated (to the surrounding air, for example, which enables us to hear the sound from a vibrating string). This dissipation of energy is called damping. We will ignore damping in our discussion.
Wave reflection
Now let’s look at wave reflection. When a wave encounters an impenetrable boundary, it gets reflected. For example, ripples on the surface of water get reflected at the edges of the water surface.

A wave travelling through a string gets reflected at the ends of the string just like light reflects from mirrors. Ideally, the reflected wave has the same displacement as the original wave, and no energy is lost during reflection.
Open and fixed ends
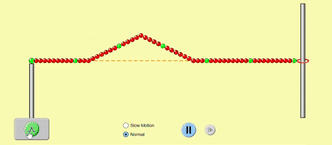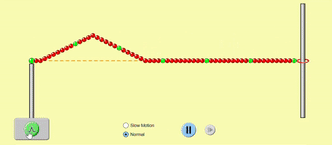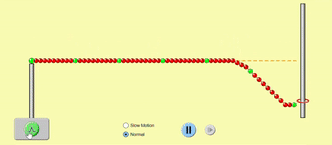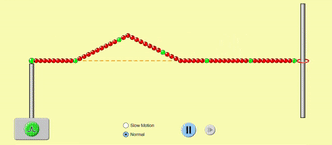
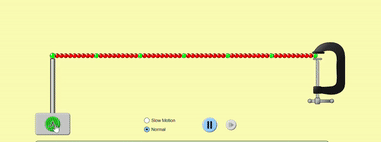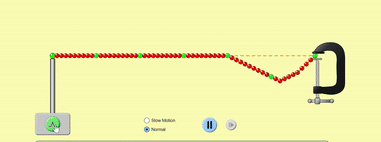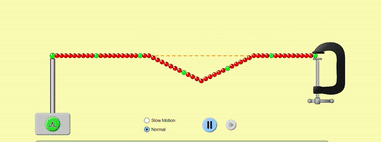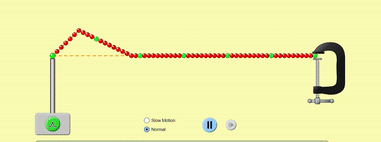
A string has two ends. These ends can be open (not fixed, free to move) or fixed (immovable). An open end reflects the wave such that the reflected wave moves back along the same path it came from, with no other changes.
Consider the GIF below. You are holding the left end of the string, and the other end is free to move. When you cause a small disturbance in the string at the left end, the disturbance travels through the string along its length towards right, and gets reflected at the open end and travels back towards left. If you sent an upright pulse, you get an upright pulse back, whereas if you send an inverted pulse, you get an inverted pulse in the reflection. Because the string is stretched and has a tension, the open end always comes back to its mean position once the pulse is reflected.
A fixed end, however, flips the wave over, so that it goes back along the same path it came from, but with the opposite displacement of the original wave.
In musical instruments, the strings always have fixed ends, and this kind of reflection at fixed ends with reversal of displacement is what we will consider in detail.
Now that we know how waves propagate and reflect on a stretched string, we will build upon this to understand what happens when we pluck a guitar string.
In the next article, we will look at some important characteristics of a wave, which will help us with further exploration of waves.
(All simulations using PhET, University of Colorado Boulder)