This is the first in a series of articles, ‘How String Instruments Work’, about the mechanics of stringed instruments without a heavy mathematical approach. We will look at wave propagation in stretched strings, and eventually build our concepts around harmonics, timbre, and audio spectra. Forget the jargon; we’re keeping it straightforward. This isn’t a maths class; it’s an adventure into the fundamentals behind the music you love. So, let’s strip away the complexities and uncover the simple beauty in the way strings make music.
In this post, we will look at the basics: wave propagation in stretched strings.
How do string instruments make sound?
String instruments vary considerably in their sound characteristics and musical range. What makes them so varied is the diverse methods of playing (bowing, plucking, striking), materials of the string (steel, nylon, brass) and body (wood from specific trees, wax, metal frets, gourds as resonators, plastic, resins), and styles of music that vary across regions and genres. This perplexing diversity is, however, unified by a few principles that are central to all string instruments, whether it is veenas from southern India, kora from Gambia, erhu from China, or pianos and violins from Europe. Many of the concepts discussed here can be extended beyond string instruments too.

Waves on a string
Waves can propagate on stretched strings because of the tension in the string, which causes it to return to its original position. When you pluck a stretched string, you supply a quick burst of energy to displace the string from its mean ‘resting’ position and then release it immediately. The string comes back to its mean position, and the displacement is transferred to an adjacent portion of the string. Mechanical energy stored in this displacement moves along the length of the string. This constitutes a transverse wave on a string.
Let us think about a much simpler string, where you are holding one end of the string, and the other end is far, far away from you (so we can ignore wave reflection for now). In the GIF below, the string is shown as going into the distance through a window. When you cause a small disturbance in the string at the left end, the disturbance travels through the string along its length towards right.
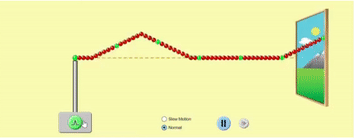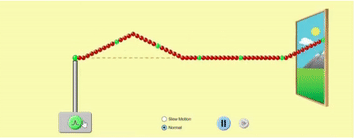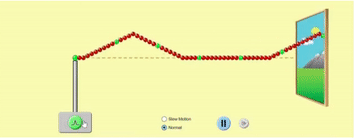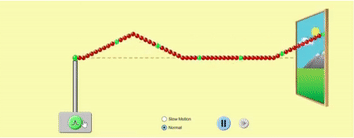
Next, we will look at strings of finite length and see how the wave is reflected at the ends.

